Tema 12: concordancia y correlación
Relación entre dos variables cuantitativas.
Una variable cuantitativa toma valores que son cuantificables, por ejemplo la talla de una persona, el peso...
Regresión lineal simple: correlación y determinación.
• -Ecuación
de la recta: y = a + bx (ej:
TAS=a +b· edad)
• -Pendiente
de la recta → b
•
Punto
de intersección con el eje de coordenadas → a
•“b”
expresa la cantidad de cambio que se produce en la variable
dependiente
por unidad de cambio de la variable independiente.
•“a” expresa cuál es el valor de la variable dependiente (eje y) cuando la independiente vale cero (eje x).
Si x=0 → y= a
• Modelos
lineales deterministas: la variable independiente determine el valor de la
variable dependiente. Entonces para cada valor de la variable independiente
sólo habría un valor de la dependiente.
Modelos lineales probabilísticos: Para cada valor de la variable independiente existe una distribución de probabilidad de valores de la dependiente, con una probabilidad entre 0 y 1.
La recta a determinar es aquélla con la menor distancia de cada punto a ella.
Coeficiente de Correlación de
Pearson.
Por lo que ya podemos decir que, si la “r” es menor que 0, tenemos una relación lineal inversa. Si la “r” es mayor de 0, la relación es lineal directa, y si “r” es igual a 0, podemos tener unas variables independientes o por otro lado una relación que no sea lineal
| | ANÁLISIS DE RELACIÓN ENTRE DOS VARIABLES CUANTITATIVAS: MODELO DE REGRESIÓN. La recta tiene una ecuación que sería: y=a+bx; aesta ecuación la vamos a llamar Modelo de regresión. Y los términos que aparecen en ella, tenemos “X” e “Y”, que son las variables. • El termino “b” es el coeficiente que va a acompañar a la “X”, el cual vamos a llamar coeficiente de regresión. • Indica cuanto cabe esperar que cambie la respuesta por cada incremento unitario de la “X”. Es decir indica la pendiente o inclinación de la recta. • También aparece un término independiente que sería “a”, (punto de intersección con el eje de coordenadas) el cual indica lo que vale la variable respuesta cuando la “X” es cero. Cuando la “X” es cero, el producto seria cero, y la “y” seria igual a “a” (y=a).  ANALISIS DE RELACIÓN ENTRE DOS VARIABLES
CUANTITATIVAS: MODELO DE REGRESIÓN. Calculamos los valores de “a” y “b” que proporcionan la recta que mejorse
ajusta. • Se parte de un criterio, y el más utilizado es el criterio de los mínimos
cuadrados. Que consiste en obtener un punto sobre la grafica que se
denomina (Yi), que es el punto observado, y posterior mente en coger un
punto sobre la recta que hemos dibujado, denominado (Yi*), este punto es
el que estima el modelo. • A continuación se calcula la diferencia entre ambos y nos interesa que la
diferencia sea lo más pequeña posible, por eso se llama el criterio de los
mínimos, y también se denomina cuadrado porque se calcula con un
término al cuadrado. • Se trata de la recta que hace mínimo el cuadrado de la suma de las
distancias verticales desde ella hasta cada uno de los puntos de la nube |
• Coeficiente
de correlación (Pearson y Spearman):
Número adimensional (entre -1 y 1) que mide la fuerza y el sentido de la
relación lineal entre dos variables.
•Coeficiente de determinación: número adimensional (entre 0 y 1) que dá idea de la relación entre las variables relacionadas linealmente. Es r2
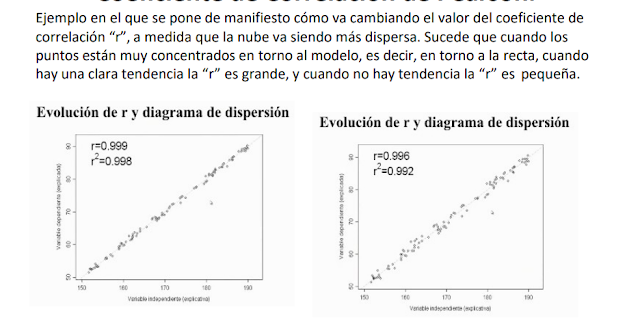
Coeficiente de correlación de Pearson.
¿COMO EVALUAMOS LA BONDAD DE AJUSTE DE ESTE MODELO?
A través de un coeficiente, que se denomina como Coeficiente de Determinación y se denota normalmente como R2. Ese valor esta acotado entre 0 y 1. Cuanto más se aproxime a 1, mayor poder explicativo, mayor bondad de ajuste, es decir más cantidad de puntos de la nube están cerca realmente ese modelo. En la práctica solemos presentarlo multiplicado por 100.
Comentarios
Publicar un comentario