Tema 4: introducción a la estadística descriptiva

INTRODUCCIÓN A LA ESTADÍSTICA DESCRIPTIVA: Medidas resumen variables cualitativas. Medidas de frecuencia. Proporciones, razones y tasas. Construcción de tablas de frecuencia

Estadística descriptiva

Los procedimientos están dirigidos a la organización y descripción de un conjunto de datos. 

Organiza de manera clara y fácil de analizar, resume los datos, explora la relación entre variables y es preliminar antes de la inferencia. Ademas, es el tipo de estadística que normalmente vemos en los medios de difusión.

Estadística inferencial

Utiliza muestras de datos para sacar conclusiones sobre poblaciones más grandes.

Este tipo de método se encuentra más frecuentemente en artículos publicados sobre investigación científica.

Infiere o “induce” leyes de comportamiento de una población, a partir del estudio del análisis de una muestra.
Apoyándose en el cálculo de probabilidad y a partir de datos muestrales, efectúa:
– Estimaciones
– Decisiones
– Predicciones
– Generalizaciones sobre un conjunto mayor de datos.

Variables: presentación de datos

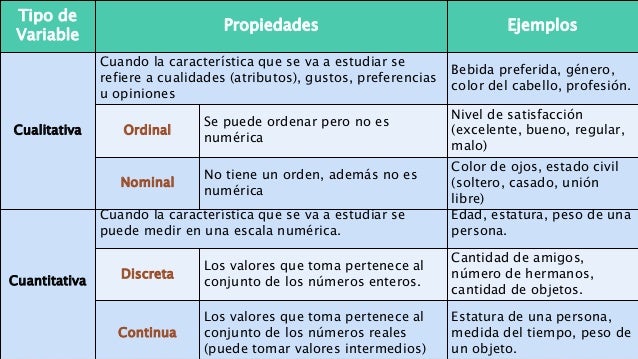
A modo de resumen como vimos en la entrada anterior, las variables se pueden clasificar en:

A su vez, la variable cualitativa nominal se puede dividir en dicotómica y policotómica.

Tablas de frecuencia

Datos que muestran frecuencias en columnas y las categorías de las variables en las filas.
Presentan información repetitiva de forma visible y comprensible.

• Requisitos:

Son autoexplicativas.

Son sencillas y de fácil compresión.

Tienen título, breve y claro.

Indican lugar, fecha  y fuente de información.

Incluye las unidades de medida en cada cabecera.

Indicas frecuencias absolutas y relativas.

¿Cómo hacer una tabla de frecuencia para datos no agrupados?

¿Cómo hacer una tabla de frecuencia para datos agrupados?

Variables continuas

- Definición de intervalos.

- Definición de extremos de los intervalos.

- Definición de amplitud o distancia entre los extremos.

- Cálculo de la marca de clase de cada intervalo.

La manera de hacerlo sería la siguiente: 

1. Calculamos el recorrido (rango,R), diferencia entre el mayor y el menor de los datos de una distribución estadística. 
2. Cuando no nos dice nada del nº de intervalos, se obtiene calculando la raíz cuadrada del nº de datos observados. El resultado será el número de intervalos.(K)
3. La amplitud (A) del intervalo se calculará dividiendo el rango entre el numero de intervalos. A=R/K.

- Frecuencia absoluta: número de individuos que presentan una modalidad, o que están incluidos en un intervalo

- Frecuencia relativa: proporción de individuos referidos al total que presentan una modalidad o que están incluidos en un intervalo

- Frecuencias acumuladas: número de individuos menores o iguales que la modalidad o el intervalo que estamos estudiando.

Indicadores/concepto de indicador

En el análisis descriptivo se usan en gran medida los números relativos, que son la expresión de la relación de dos o más cantidades.

La frecuencia absoluta no puede ser un indicador, pues le falta un denominador que la relacione con el tamaño de la muestra o población, y/o el período en el que se presentaron los eventos.

Se define indicador como la medida de la frecuencia de un determinado suceso en una población, expresado como un número que puede ser:

- Proporción.

- Tasa.

- Razón.

- Odds.

Los indicadores siempre están formados por un numerador y un denominador, es decir, es el resultado del cociente entre dos magnitudes.

• Proporción

Se define como una medida resumen para variables cualitativas, que consiste en la comparación, a través de un cociente (división) entre un subconjunto y el conjunto al que pertenece.

Características a tener en cuenta:

1. El numerador siempre está incluido en el denominador.
2. Adopta valores reales entre 0 y 1, expresando la frecuencia relativa del suceso que medimos.
3. Se suele multiplicador por 100, para calcular una mejor compresión, expresando los porcentajes correspondientes.
4. Si el suceso que medimos es muy poco frecuente, podemos multiplicar por 1000, por 10000, etc.

• Tasa (RATE)

Es una medida que expresa el riesgo de ocurrencia del evento estudiado.

En realidad, es una proporción pero con relación espacial y temporal. El denominador incluye una unidad de tiempo.

Consiste en la comparación, a través de una división, entre el número de veces que ocurre un cierto tipo de evento y la población en la que puede ocurrir dicho evento en un tiempo determinado.

Usualmente el resultado de tal división consiste en una cifra fraccionaria menor a 1, por lo que el resultado suele ser multiplicado por alguna constante que sea múltiplo de 10.

Medidas más empleadas en estadística sanitaria

• Prevalencia: describe qué proporción de la población tiene la enfermedad en un punto específico en el tiempo. Depende de la velocidad de aparición de la enfermedad (incidencia) y de su duración.

• Incidencia: es el número de casos nuevos de una enfermedad que ocurren en un período específico de tiempo, en una población a riesgo de desarrollar la enfermedad. La incidencia mide cambio: de ausencia a presencia de enfermedad, de vivo  a muerto, de no tener una característica a tenerla. La incidencia es una medida de riesgo.

Podemos distinguir entre: 

-Incidencia acumulada (proporción de incidencia): riesgo de que se produzca el suceso.

-Tasa de incidencia (densidad de incidencia): velocidad de aparición de nuevos casos con respecto al tamaño de la población.

Incidencia acumalada (proporción de incidencia)

Se calcula utilizando un período de tiempo durante el cual consideramos que todos los individuos de la población están a riesgo de la enfermedad.

Es la proporción de sujetos que desarrollan la enfermedad, en un período de tiempo, del total de la población a riesgo al inicio del período.

Mide el riesgo promedio de padecer la enfermedad (probabilidad de desarrollar la enfermedad).

IA= Nuevos casos en un tiempo determinado/ población a riesgo en t0 (tiempo inicial).

1. Mide la probabilidad de tener la enfermedad (evento)
2. No tiene unidades. Es una proporción ( se expresa como %...)
3. Valores entre 0 y 1.
4. No lleva implícito el período de tiempo, con lo cual debe expresarse siempre.

Condiciones:

- No puede haber pérdidas en el seguimiento.

- Se siguen a todos los sujetos durante todo el período.

- No permite inferir fuera del período de estudio.

Tasa de incidencia (o densidad de incidencia).

Con frecuencia, no todos los individuos a riesgo ( denominador), son seguidos durante el mismo período de tiempo.

Si se disponen de los diferentes tiempos de observación de los diferentes individuos, se puede calcular la densidad de incidencia o tasa de incidencia.

Es necesario especificar la unidad de tiempo a las que se refiere la tasa (personas- año; personas-mes, personas- semana, etc).

Pautas:

1. Se mide en unidades de tiempo (-1).
2. No son proporcionales, es una tasa instantánea.
3. Expresa la "tasa" a la cual ocurren los eventos en sujetos de la población en riesgo en cualquier momento.
4. Expresa la velocidad: la tasa de cambio instantáneo o la rapidez con la que se desarrolla el evento en la población.

- Tasa: datos agregados.

- Densidad de incidencia: tasa obtenida de datos individuales.

Densidad de incidencia basada en datos individuales.

Densidad de incidencia= nuevos casos/ personas- tiempo a riesgo.

Personas - tiempo:

- Suma de tiempos que los individuos están a riesgo de desarrollar el evento.

- Las unidades a utilizar dependen del investigador. Los eventos poco frecuentes suelen describirse en personas- año o un múltiplo del mismo (100 o 1000 personas - año). En cambio, en los eventos más frecuentes se pueden utilizar personas- semana o personas- día.

 Adjunto un vídeo resumen sobre la prevalencia, incidencia y tasa de incidencia 

• Razones o "ratios"

Es una medida de resumen para variables cualitativas que consiste en la comparación, a través de una división entre dos conjuntos.

Los dos conjuntos son distintos, es decir, uno no incluye al otro.

El numerador del cociente, por tanto, no está incluido en el denominador, como sí sucedía en las proporciones.

Ejemplo: La razón de sexos: 

En una empresa trabajan 1.200 hombres y 345 mujeres. La razón de sexos será de 1.200/345, es decir, 3,47 hombres por cada mujer, o 347 hombres por cada 100 mujeres

• Odds o ventaja

El cociente entre la proporción o probabilidad de ocurrencia de un evento y la probabilidad (complementaria) de no ocurrencia, se denomina con el término en inglés "odds", empleado en el lenguaje de apuestas.

No hay un término exacto en español, no consenso en su traducción. El más aceptado es "ventaja" u "oportunidad".

La odds representa la frecuencia de un aspecto relativa a los sujetos que no presentan dicho aspecto, por lo que es un tipo especial de razón.

Sus valores van desde 0, que serían eventos que nunca ocurren, hasta infinito, que serían los que ocurren con mucha frecuencia.

Medidas de asociación: relaciones entre proporción, ratios y odds.

La magnitud de asociación entre dos fenómenos, puede estimarse a través de medidas que relacionen proporciones, tasas y odds.

Es lo que se llaman "medidas de asociación" y dependiendo del tipo de estudio, se usarán una u otra.

Las tres partes más importantes son:

• Razón de prevalencias: estudios descriptivos de corte transversal. Realiza una ratio entre dos prevalencias (proporciones). Es la razón entre la proporción de enfermos expuestos y la proporción de enfermos no expuestos. Cuantifica una estimación de la asociación enre el factor de exposición y la enfermedad.

Si el valor se aproxima a 1, la enfermedad se distribuye por igual entre los expuestos y los no expuestos.

R.p.= P.e/P.ne. MAGNITUD DE LA ASOCIACIÓN.

• Riesgo relativo o razón de riesgos: estudios de observaciones de seguimiento o estudios experimentales. Realiza un ratio entre dos incidencias acumuladas (proporciones) o dos densidades de incidencia (tasas). Es la razón entre el riesgo en los expuestos y el riesgo en los no expuestos. Cuantifica el incremento en el riesgo producido por la exposición.

Si el valor se aproxima a 1, la enfermedad o el suceso aparece de forma similar entre los expuestos y los no expuestos.

RR= I.e/ I.ne. MAGNITUD DE LA ASOCIACIÓN.

• Odds ratio: estudios de casos y controles. Realiza una ratio entre dos medidas odds.  Es la razón entre los odds de los casos y los odds de los controles.

O.R.= ODDS Casos/ ODDS Controles

Valores posibles de 0 a 1.